TRIANGOLI RETTANGOLI
TEORIA IN PILLOLE
Un problema tipo
Condotta per A, estremo del diametro AB di una
semicirconferenza, una corda AC, determina l'ampiezza dell'angolo
CAB = x in modo tale che AC + 2 CH = 4r, dove H è la proiezione
di C sulla tangente in B alla semicirconferenza.
RISOLUZIONE
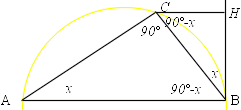
- Fare un disegno chiaro inserendo non solo i dati ma anche le
altre informazioni dedotte da quanto rappresentato. L'angolo x
è assimilato ad un dato noto.
- Definire l'insieme di variabilità dell'incognita x.
- 1° CASO LIMITE C=B CAB=x=0
- 2° CASO LIMITE C=A=x=90°
Casi ordinari 0°<x<90°
- Si determina immediatamente AC=2r cos x
- CH = CB senx
- CB=2r senx
- CH=2r sen2x
Equazione associata alla condizione imposta:
2r cosx + 4r sen2x = 4r (dividere tutto per 2r)
cos x + 2 sen2 x= 2
cos x + 2(1- cos2 x)= 2
2 cos2 x - cos x =0
Soluzioni:
cos x = 0 x = 90° (caso limite)
cos x = 1/2 x = 60° (caso ordinario) |
Altri problemi da risolvere
| 1° |
Determinare l'angolo ACB = x di un
triangolo rettangolo ABC, retto in A, sapendo che è (2AB +
3AC)/(AB + AC)=7/3 |
| 2° |
Determinare, sulla semicirconferenza di centro
0 e diametro A = >2r, un punto C in modo che sia
verificata la relazione: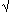 3
AC + 3 CO = 3 AB |
| 3° |
Nel triangolo equilatero ABC di lato L, si conduca dal vertice
B la semiretta interna al triangolo in modo che BM + CN = L,
dove M e N sono rispettivamente le proiezioni di B e di C sulla
semiretta. |
| 4° |
In un triangolo rettangolo il rapporto tra il perimetro e
l'altezza relativa all'ipotenusa è 2(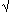3
+ 1) . Calcolare le ampiezze degli angoli. |
| 5° |
Su una semicirconferenza di diametro AB= 2r prendi un punto Q
tale che detta M la sua proiuezione sul diametro AB, sia 4 AM
+MQ=5r |
|