Christopher Kent Mineman - Didattica in rete

1° ESEMPIO

Risolvere l'equazione tgx + 2senx = 0

essa è equivalente a + 2senx = 0

bisogna allora porre la condizione cosx0 cioè xπ/2+2kπ, quindi svolgendo i calcoli:
sen x + 2senx cosx = 0
sen x( + 2cos x) = 0
che dà senx = 0 e cosx = -

e quindi x = kπ x = + + 2kπ

SECONDO ESEMPIO

Risolvere l'equazione cos2x - 2senx = cos²x

applicando le formule di duplicazione si ottiene:

cos²x - sen²x - 2senx = cos²x

e quindi

sen²x + 2senx = 0
senx (sen x + 2) = 0
da cu senx = 0 e senx = -2

la prima delle due avrà soluzione x = kπ (con k = +1, +2, +3, .....) , la seconda è invece impossibile.

Omogenea di primo grado

senx + cosx= 0

dividendo il primo e il 2° membro per cosx si ha:

tgx = - e quindi: x = + kπ

Omogenea di secondo grado

sen²x + cosx(senx + cosx) = cos²x

sen²x + cosxsenx = 0

essendo un'equazione di 2° grado si

divideranno entrambi i membri per cos²x ottenendo:

tang²x + tangx = 0

 da cui si ricava: tang x = 0 e tang x = -

dalla prima si ottiene: x = kπ

dalla seconda: x = -π/6 + kπ o, equivalentemente: x = + kπ

equazioni lineari (normalmente al posto di tang (x/2) sostituiremo la variabile t.

è evidente che l'uguaglianza non è soddisfatta per i valori x=p+2kπ Quindi si sostituiranno sen x e cos x con le corrispondenti espressioni in funzione di tg(x/2):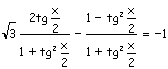

da cui si ricava:

2

tg(x/2) = 0

tg(x/2) = -

da queste si ricava:

x = 2kπ

x= = - + 2kπ