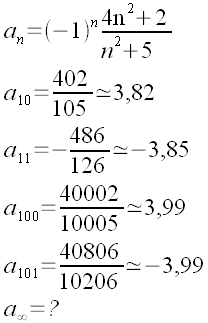Consideriamo una successione del tipo an = f(n), dove con f(n) si intende una espressione algebrica contenente la variabile n.
Abbiamo varie scritture ad esempio:
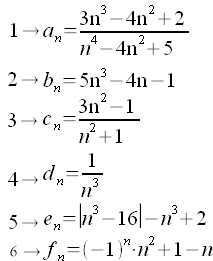 |
|
| 1) La successione è associata ad una funzione razionale fratta (3o grado su 4o grado). | |
| 2) la successione è associata ad un polinomio di 3o grado. | |
| 3) La successione è associata ad una funzione razionale fratta (2o grado su 2o grado). | |
| 4) reciproco di n al cubo | |
| 5) polinomio contenente termine in valore assoluto. | |
| 6) Successione a termini scillanti (+/-) |
Cosa accade all'infinito?
Se considero una qualsiasi successione, conoscendo il legame che lega l'elemento con il corrispettivo numero naturale [ an = f(n) ], mi posso porre la domanda: che valori assume quando considero n sempre più grandi?
Analizziamo le seguenti successioni:
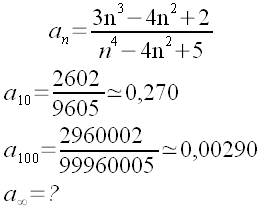 |
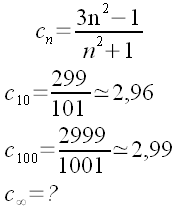 |
| Inoltre: | |
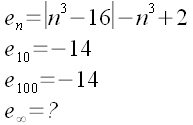 |
|
| Ed infine: | |
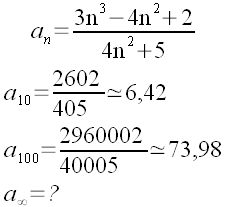 |
Cosa possiamo dedurre da queste analisi?
Le successioni si comportano diversamente.
Alcune volte sembra che si avvicinino ad un valore, altre volte tendono a valori sempre più grandi.
Chiameremo successioni convergenti le prime e divergenti le seconde.
Studieremo ora il comportamento delle successioni quando n si avvicina all'infinito e introdurremo il concetto di limite.