Segmenti e punti
Per affrontare i problemi di geometria analitica dobbiamo unire le conoscenze delle proprietà deipoligoni, rette e angoli, con le regole ora studiate.
1° esercizio
Calcolare il quarto vertice e il perimetro del parallogramma avente tre consegutivi nei punti A(3;1) - B(-4;2) C(7;7).
Dobbiamo determinare il quarto vertice. Come?
Proprietà del parallelogramma:
1° |
Lati opposti paralleli |
2° |
Lati opposti congruenti |
3° |
Le diagonali si bisecano |
4° |
Angoli opposti congruenti |
5° |
Angoli adiacenti supplementari |
Per calcolare il quarto vertice sfrutteremo la terza proprietà (conosciamo solo le formule della distanza fra due punti e quella del punto medio).
Il punto medio della diagonale AC coincide col punto medio della diagonale BD e quindi
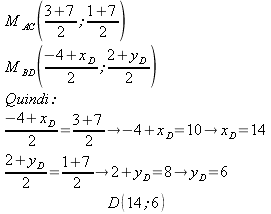
Per determinare il perimetro sfruttiamo la seconda proprietà e quindi determiniamo la lunghezza di due lati adiacenti:
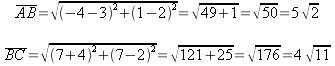 |
Infine determiniamo il perimetro:
2° esercizio
Determinare il perimetro del triangolo avente per vertici e punti medi dei segmenti AB, BC, CA essendo A(-2;3) B(1;4) C(7;6)
Esercizio banale: basta calcolare le coordinate dei tre punti medi e quindi la distanza dei tre segmenti.
Coordinate dei tre punti medi (utilizzo la formula del punto medio):
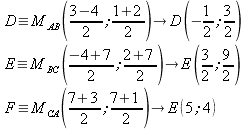 |
Determino le lunghezze dei tre lati:
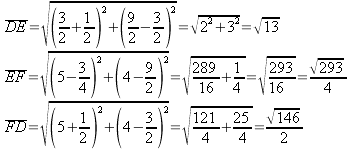 |
Perimetro:
3° problema
Determinare il punto appartenente all'asse delle x tale che la distanza dal punto A(3;4) sia uguale alla distanza dal punto B(-3;5).
Il punto generico appartenente all'asse x ha coordinate generiche P(XP;0).
Per determinare le coordinate di questo punto bisogna imporre che PA=PB e quindi:
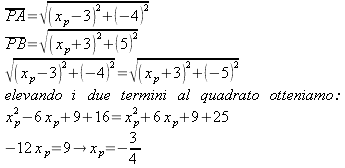 |