.. Campo elettrico prodotto da una sfera
Utilizzando il teorema di Gauss dimostreremo che una sfera conduttrice uniformemente carica da origine ad un campo elettrico il cui vettore di intensità all'esterno della sfera è equivaente a quello prodotta da una carica puntiforme posta al centro della sfera e su cui sia posta la stessa carica distribuita sulla sfera.
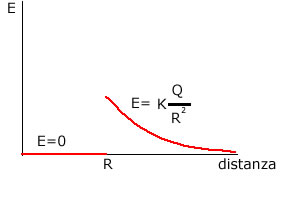
All'interno della sfera il campo è nullo.
Prendiamo per superficie su cui calcolare il flusso totale uscente una sfera 
concentrica con la sfera carica e avente un raggo maggiore del ragio della sfera.
Sperimentalmente osserviamo che le linee di forza sono tutte radiali ed uscenti dalla sfera ed inoltre il valore di E (per motivi di simmetria, anche se ruoto la sfera il campo non si modifica) ad uguale distanza dal centro assume sempre lo stesso valore.
Suddividiamo la superficie della sfera in n superfici elementari dS così piccole che siano praticamente piane, per cui il campo elettrico uscente risulti essere sempre costante in modulo, direzione e verso, in ogni punto di dS.
Ricordiamoci che la normale a ciascuna superficie
è sempre parallela alle linee del campo in ogni punto della stessa superficie. Sappiamo che il flusso
attraverso ciascuna superficie Δ S è dato dal
prodotto del campo elettrico per la superficie per il coseno dell’anglo
formato dal vettore campo elettrico e la normale alla superficie che,
essendo paralleli, è sempre 1. Perciò il flusso totale sarà
dato dalla somma dei flussi parziali, ovvero di ciascun flusso attraverso
ciascuna superficie cioè: 
; quindi essendo E costante lo possiamo raccogliere a fattor comune e otteniamo: 
Ricordandoci che per il teorema di Gauss il flusso totale uscende dalla sfera è 
, possiamo determinare immediatamente quanto vale l'intensità del campo elettrico in ogni punto, all'esterno della sfera: 
.
Per determinare il campo all'interno della sfera, rifacciamo lo stesso ragionamento utilizzando una superficie sferica di raggio inferiore a quello sella sfera.
Abbiamo per il teorema di Gauss che il flusso totale uscente è nullo e dovendo essere contemporaneamente uguale a , si ricava che E=0.
Riportando su un piano cartesiano l'andamento del campo elettrico si ottiene:
