Testo

Assegnato un punto appartenente al piano determinare in quale posizione sarà minima l'ordinata imponendo che la somma dei quadrati delle distanze dai punti A(3;1) e B(-3;9) deve essere uguale a 2 volte il quadrato della distanza del punto dall'asse x.

Impostazione problema

Si prende per variabile doppia il punto P(a;b). Non essendoci vincoli porremo:

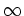• - < a < +
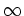
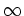• - < b < +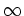

Determiniamo ora le distanze:

Risoluzione

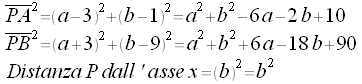
Ora ricaviamo la relazione:

:

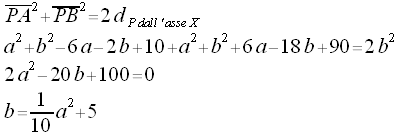
pertanto

La relazione trovata è associabile all'equazione di una parabola con la concavità rivolta verso l'alto in un sistema di assi cartesiani a,b. Il punto di ordinata minima appartenente a tale luogo geometrico avente l'ordinata minima è il vertice di coordinate (0;5).

Conclusione

Il punto richiesto (ricordandoci che a=x e b=y) è P(0;5).