DEFINIZIONE: Parabola è il luogo geometrico dei punti del piano equidistanti da un punto fisso chiamato fuoco e da una retta chiamata direttrice. Studieremo per il momento solo le parabole aventi per direttrici rette parallele all'asse delle ascisse. Queste parabole sono associate alle funzioni del tipo: y=ax2+bx+c |
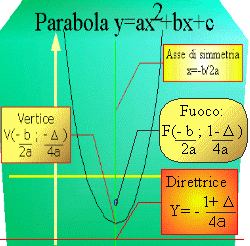 |
Come impostare i problemi
per ricavare l'equazione della parabola
determinando i valori di: a - b - c
| Passaggio per punto assegnato | Sostituire nell'equazione generica alle variabili x e y i valori delle corrispondenti coordinate. Si ottiene un'equazione nei tre parametri a,b,c. |
| Vertice assegnato | Si ottengono 2 condizioni:
|
| Fuoco assegnato | Si ottengono 2 condizioni:
|
| direttrice assegnata | 1 Condizione:
|
Tre parametri - tre condizioni.
Mettere a sistema le tre equazioni ricavate e determinare i valori dei tre parametri.
Parabola-retta
Assegnata una retta e una parabola possiamo avere:
- Retta esterna. Non interseca mai la parabola.
- Retta secante. Interseca la parabola in due punti distinti.
- Retta tangente. Ha in comune con la parabola un punto doppio.
A livello algebrico:
Trovare le intersezioni significa porre a sistema le equazionbi dei due luoghi geometrici.
Essendo un sistema tra un'equazione di 1° grado ed una di 2° grado l'equazione risolvente è di 2° grado (nel nostro caso in x) e pertanto se:
| D>0 | l'equazione ammette due soluzioni distine. Il sistema ammette due soluzioni. LA RETTA E' SECANTE |
| D=0 | L'equazione ammette due soluzioni coincidenti. LA RETTA E' TANGENTE |
| D<0 | L'equazione non ammette nessuna soluzione reale. LA RETTA E' ESTERNA |