Dagli esperimenti di Rutherford abbiamo visto che un atomo può essere visto come un oggetto costituito da un nucleo contenente la carica positiva schermato nello spazio circostante dagli elettroni di carica negativa. L'atomo globalmente è neutro in quanto la somma delle cariche positive è contobilanciata dalla somma delle cariche negative.

In prima approssimazione è risultato utile considerare l'atomo come un sistema planetario in cui il nucleo si comporta come il sole e gli elettroni come i pianeti.

Dal modello planetario all'atomo di Bohr

Un elettrone ruota attorno ad un atomo come un pianeta attorno al sole. Nel caso più semplice di un elettrone che ruota attorno al nucleo di moto circolare uniforme, si osserva che l'elettrone è in grado di rimanere in orbita attorno al nucleo solo se la forza centripeta risulta essere  controbilanciata dalla forza centrifuga dovuta allo stesso moto circolare uniforme.

Forza centripeta = Forza elettrostatica = K e² / R²

Forza centrifuga = m V² / R

In queste condizioni esso potrebbe stazionare a qualsiasi distanza dal nucleo, ma questo contrasta sia con quanto previsto dalla teoria sia dagli eventi sperimentali.

1. Un elettrone che accelera in un campo elettrico deve perdere energia e di conseguenza cadere sul nucleo dopo pochi secondi.

2. Un elettrone che perde energia trasferisce la stessa a un fotone di energia hn, energia pari a quella persa dall'elettrone, quindi lo spettro dell'atomo d'idrogeno dovrebbe essere continuo e non a righe come verificato sperimentalmente.

Bohr e la quantizzazione del momento angolare

Per superare quanto sopra contestato, Bohr ha ipotizzato che, per motivi non meglio precisati, un elettrone può permanere indefinitamente solo su orbite che rispettano le seguenti condizioni:

1. K e² / R²  = m V² / R

2. Il momento della quantità di moto deve essere quantizzato ossia: mVR = n h (h costante di Plank)

Imponendo tali condizioni si ricava:

K e² / R²  = m V² / R

K e² = m V² R

m K e² R = ( m V R)² = (nh)²

R= n² [ h² / (m K e²)] = n² R₀

essendo i termini racchiusi tra le parentesi quadre tutti associati a costanti si ricava che il raggio ossia la distanza dal nucleo in cui si può trovare un elettrone risulta essere proporzionale a n ( numero appartenente a N) al quadrato.

L'energia totale di tale elettrone è pari alla metà dell'energia potenziale e quindi:

E(n)= - 1/2 K e² / R = - 1/n² [ 1/2 m K² e⁴ / h²] ossia inversamente proporzionale all'inverso del quadrato di n.

L'energia rilasciata da un elettrone che passa da un livello n₂ a un livello n₁ con la creazione di un fotone di energia hn = E(n₂) -E(n₁)

ossia: n = R_H ( 1/n₁² -1/n₂²) si osserva sperimentalmente quando consideriamo l'atomo di idrogeno.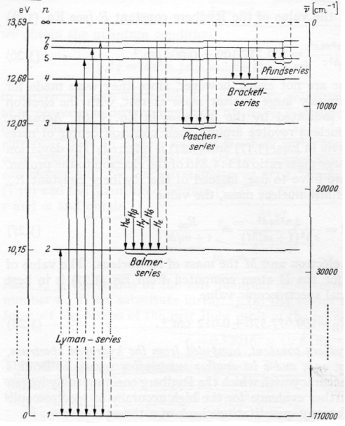

• Quanto ricavato non vale per gli altri atomi. Perchè?
• Perché si deve quantizzare il momento della quantità di moto?

Non esistono limiti e pertanto si possono prevedere livelli a distanza infinita dal nucleo (considerando n tendente all'infinito).

Pertanto quanto ricavato vale solo per i gas. Cosa accade se vogliamo applicare quanto ricavato ad una sostanza contenente numerosissimi atomi a distanze reciproche dell'ordine dei 10^-10 metri?