Pur avendo struttura di campo l'insieme dei numeri razionali, non è possibile definire in Q l'operazione inversa dell'operazione potenza ( la radice ennesima di un numero) e altre operazioni su operatori particolari (seno, logaritmo, ... ).

Dato un numero naturale è sempre possibile calcolare la sua potenza.

Ad esempio ed è possibile effettuare l'operazione inversa e possiamo pertanto scrivere

E' possibile effettuare l'operazione inversa e calcolare la 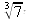? Ossia è possibile calcolare quel numero y che soddisfa la seguente condizione: .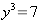

Premesso che dobbiamo trovare quel numero razionale che soddisfi quanto richiesto.

Operando per tentativi ricaviamo:

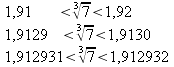
Possiamo determinare infiniti numeri decimali minoranti e maggioranti che sempre meglio aprossimano il numero cercato, ma non possiamo determinare la .

Definiamo numero reale assoluto quel numero che può essere considerato elemento separatore di una partizione di Q⁺.

Nel caso in esame possiamo suddividere tutti i numeri razionali in due sottoinsiemi, il primo dei numeri razionali il cui cubo è inferiore a 7, il secondo costituito da tutti i numeri razionali maggiori di 7.

Non troveremo mai il numero razionale il cui cubo sia esattamente uguale a 7.

Possiamno ipotizzare che debba esistere un numero "strano" non razionale il cui cubo sia esattamente uguale a 7. Questo numero deve essere tale da essere l'elemento separatore dell'insieme A dei numeri il cui cubo è inferiore a sette e di tutti gli altri numeri (insieme B) il cui cubo è maggiore di 7.

I due insiemi sono tali che per ogni numero e piccolo a piacere è possibile determinare un numero appartenente all'insieme A e un secondo appartenente all'insieme B, tali che la loro differenza sia minore di e . Pertanto esiste un elemento separatore tra i due insiemi. Detto elemento separatore non è in questo caso un elemento appartenente a Q⁺ . Il numero individuato è un numero reale, e nel caso specifico (operazione inversa dell'operazione potenza) è un numero irrazionale.